Module 0 - Entry Exam v6.0
Question 1
For the following data set, calculate the mean and median.
10, 8, 5, 7, 14, 5, 3, 9, 5, 8
- A. The mean is 7.4 and the median is 7.5.
- B. The mean is 7.4 and the median is 8.0.
- C. The mean is 8.2 and the median is 7.5.
- D. The mean is 8.2 and the median is 8.0.
Answer : A
Question 2
A biased coin has the following probability distribution function:
P(heads) = 0.80 -
P(tails) = 0.20 -
The biased coin is tossed twice in succession.
Calculate the probability of tossing at least one tail.
- A. 0.20
- B. 0.36
- C. 0.64
- D. 0.80
Answer : B
Question 3
State what the limit of a function with input variable x represents.
- A. The limit represents the smallest value that the function can take over its considered range.
- B. The limit represents the behaviour of a function as x approaches a certain value.
- C. The limit represents the value of x for which the function is incalculable.
- D. The limit represents the value of the function when x=0.
Answer : B
Question 4
In a small island nation, local sea vessels are identified using "a letter and 4 digits" classification system. The "letter" can be any of the 26 letters in the English alphabet, A to
Z, while the "digit" can be any number from 0 to 9. E.g: Z9835.
Calculate the probability of a sea vessel having an identification ending in "007".
- A. 0.001
- B. 0.002
- C. 0.003
- D. 0.504
Answer : A
Question 5
Identify the meaning of: | x | > 5
- A. x is greater than 5.
- B. x is greater than or equal to 5.
- C. x is greater than 5 or x is less than -5.
- D. x is greater than or equal to 5, or x is less than or equal to -5.
Answer : C
Question 6
The probability density function f(x) for a random variable X is defined over the interval 0 to
1.
f(x) = 2(1-x).
Calculate the probability that X is greater than 0.5.
- A. 0.25
- B. 0.5
- C. 0.75
- D. 1
Answer : A
Question 7
Calculate -
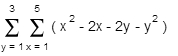
- A. -245
- B. -95
- C. -55
- D. 55
Answer : C
Question 8
v = f(x, y, z) is a real valued function of 3 variables.
Express the partial derivative of v with respect to z in standard mathematical notation.
A)
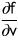
B)
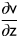
C)
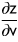
D)
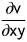
- A. Option A
- B. Option B
- C. Option C
- D. Option D
Answer : B
Question 9
Using simple iteration, based on trial and improvement, the cubic equation below can be solved:
2x3 + 5x2 +7x - 12 = 0
Solve for x to 6 decimal places.
- A. 0.909000
- B. 0.909165
- C. 0.909502
- D. 1.000000
Answer : B
Question 10
For random variable X, use the following statistics to calculate its coefficient of skewness based on central moments.
E(X) = 3.940 -
E(X2) = 21.466 -
skew(X) = E[(X - )3] = 6.008
- A. -0.415
- B. 0.060
- C. 0.415
- D. 0.768
Answer : C
Question 11
Calculate which of the following is a simplification of (1 + x)2 - x2 + ln(e3x).
- A. 1 + 2x
- B. 1 + 3x
- C. 1 + 5x
- D. 1 + 2x + x3
Answer : C
Question 12
Integrate:
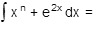
A)
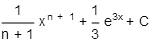
B)
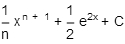
C)
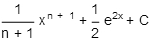
D)
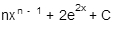
- A. Option A
- B. Option B
- C. Option C
- D. Option D
Answer : C
Question 13
Determine which of the statements is true about the root(s) of the following equation:
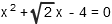
- A. There is only one real root which takes a positive value.
- B. There is only one real root which takes a negative value.
- C. There are two real roots, r1 and r2, where r1 is positive and:r1 = - 0.5 r2
- D. There are two real roots, r1 and r2, where r1 is positive and:r1 = - 2 r2
Answer : C
Question 14
The graph shows the frequency distribution of the age of people with a certain kind of insurance contract.
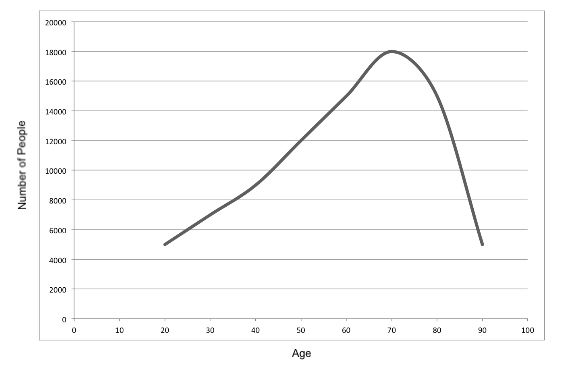
Describe the shape of the underlying data.
- A. Negatively skewed
- B. Positively skewed
- C. Symmetric
- D. Symmetric about the mean
Answer : A
Question 15
Three light bulbs are chosen at random from 15 bulbs of which 5 are known to be defective.
Calculate the probability that exactly one of the three is defective.
A)
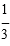
B)
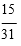
C)
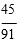
D)
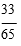
- A. Option A
- B. Option B
- C. Option C
- D. Option D
Answer : C